QUICK LINKS
BRIEF OVERVIEW
UNIT I
Purpose of Testing
Dichotomies
Model for Testing
Consequences of Bugs
Taxonomy of Bugs
Summary
UNIT II
Basics of Path Testing
Predicates, Path Predicates and Achievable Paths
Path Sensitizing
Path Instrumentation
Application of Path Testing
Summary
UNIT III
Transaction Flows
Transaction Flow Testing Techniques
Implementation
Basics of Data Flow Testing
Strategies in Data Flow Testing
Application of Data Flow Testing
Summary
UNIT IV
Domains and Paths
Nice and Ugly domains
Domain Testing
Domain and Interface Testing
Domains and Testability
Summary
UNIT V
Path products and Path expression
Reduction Procedure
Applications
Regular Expressions and Flow Anomaly Detection
Summary
UNIT VI
Logic Based Testing
Decision Tables
Path Expressions
KV Charts
Specifications
Summary
|
LOGIC BASED TESTING:
This unit gives an indepth overview of logic based testing and its implementation.
At the end of this unit, the student will be able to:
- Understand the concept of Logic based testing.
- Learn about Decision Tables and their application
- Understand the use of decision tables in test-case design and know their limitations.
- Understand and interpret KV Charts and know their limitations.
- Learn how to transform specifications into sentences and map them into KV charts.
- Understand the importance of dont-care conditions.
OVERVIEW OF LOGIC BASED TESTING :
- INTRODUCTION:
- The functional requirements of many programs can be specified by decision tables, which provide a useful basis for program and test design.
- Consistency and completeness can be analyzed by using boolean algebra, which can also be used as a basis for test design. Boolean algebra is trivialized by using Karnaugh-Veitch charts.
- "Logic" is one of the most often used words in programmers' vocabularies but one of their least used techniques.
- Boolean algebra is to logic as arithmetic is to mathematics. Without it, the tester or programmer is cut off from many test and design techniques and tools that incorporate those techniques.
- Logic has been, for several decades, the primary tool of hardware logic designers.
- Many test methods developed for hardware logic can be adapted to software logic testing.
Because hardware testing automation is 10 to 15 years ahead of software testing automation, hardware testing methods and its associated theory is a fertile ground for software testing methods.
- As programming and test techniques have improved, the bugs have shifted closer to the process front end, to requirements and their specifications.
These bugs range from 8% to 30% of the total and because they're first-in and last-out, they're the costliest of all.
- The trouble with specifications is that they're hard to express.
- Boolean algebra (also known as the sentential calculus) is the most basic of all logic systems.
- Higher-order logic systems are needed and used for formal specifications.
- Much of logical analysis can be and is embedded in tools. But these tools incorporate methods to simplify, transform, and check specifications, and the methods are to a large extent based on boolean algebra.
- KNOWLEDGE BASED SYSTEM:
- The knowledge-based system (also expert system, or "artificial intelligence" system) has become the programming construct of choice for many applications that were once considered very difficult.
- Knowledge-based systems incorporate knowledge from a knowledge domain such as medicine, law, or civil engineering into a database.
The data can then be queried and interacted with to provide solutions to problems in that domain.
- One implementation of knowledge-based systems is to incorporate the expert's knowledge into a set of rules. The user can then provide data and ask questions based on that data.
- The user's data is processed through the rule base to yield conclusions (tentative or definite) and requests for more data. The processing is done by a program called the inference engine.
- Understanding knowledge-based systems and their validation problems requires an understanding of formal logic.
- Decision tables are extensively used in business data processing; Decision-table preprocessors as extensions to COBOL are in common use;
boolean algebra is embedded in the implementation of these processors.
- Although programmed tools are nice to have, most of the benefits of boolean algebra can be reaped by wholly manual means if you have the right conceptual tool: the Karnaugh-Veitch diagram is that conceptual tool.
DECISION TABLES:
- Figure 6.1 is a limited - entry decision table. It consists of four areas called the condition stub, the condition entry, the action stub, and the action entry.
- Each column of the table is a rule that specifies the conditions under which the actions named in the action stub will take place.
- The condition stub is a list of names of conditions.
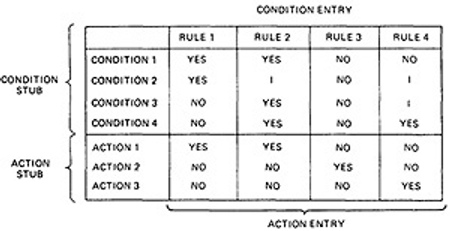
Figure 6.1 : Examples of Decision Table.
- A more general decision table can be as below:
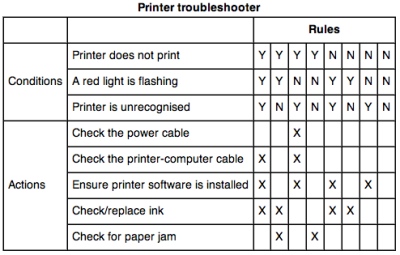
Figure 6.2 : Another Examples of Decision Table.
- A rule specifies whether a condition should or should not be met for the rule to be satisfied. "YES" means that the condition must be met,
"NO" means that the condition must not be met, and "I" means that the condition plays no part in the rule, or it is immaterial to that rule.
- The action stub names the actions the routine will take or initiate if the rule is satisfied. If the action entry is "YES", the action will take place; if "NO", the action will not take place.
- The table in Figure 6.1 can be translated as follows:
Action 1 will take place if conditions 1 and 2 are met and if conditions 3 and 4 are not met (rule 1) or if conditions 1, 3, and 4 are met (rule 2).
- "Condition" is another word for predicate.
- Decision-table uses "condition" and "satisfied" or "met". Let us use "predicate" and TRUE / FALSE.
- Now the above translations become:
- Action 1 will be taken if predicates 1 and 2 are true and if predicates 3 and 4 are false (rule 1), or if predicates 1, 3, and 4 are true (rule 2).
- Action 2 will be taken if the predicates are all false, (rule 3).
- Action 3 will take place if predicate 1 is false and predicate 4 is true (rule 4).
- In addition to the stated rules, we also need a Default Rule that specifies the default action to be taken when all other rules fail. The default rules for Table in Figure 6.1 is shown in
Figure 6.3
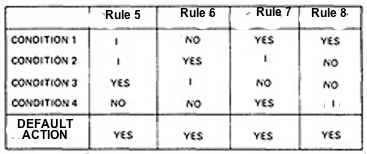
Figure 6.3 : The default rules of Table in Figure 6.1
- DECISION-TABLE PROCESSORS:
- Decision tables can be automatically translated into code and, as such, are a higher-order language
- If the rule is satisfied, the corresponding action takes place
- Otherwise, rule 2 is tried. This process continues until either a satisfied rule results in an action or no rule is satisfied and the default action is taken
- Decision tables have become a useful tool in the programmers kit, in business data processing.
- DECISION-TABLES AS BASIS FOR TEST CASE DESIGN:
- The specification is given as a decision table or can be easily converted into one.
- The order in which the predicates are evaluated does not affect interpretation of the rules or the resulting action -
i.e., an arbitrary permutation of the predicate order will not, or should not, affect which action takes place.
- The order in which the rules are evaluated does not affect the resulting action -
i.e., an arbitrary permutation of rules will not, or should not, affect which action takes place.
- Once a rule is satisfied and an action selected, no other rule need be examined.
- If several actions can result from satisfying a rule, the order in which the actions are executed doesn't matter
- DECISION-TABLES AND STRUCTURE:
- Decision tables can also be used to examine a program's structure.
- Figure 6.4 shows a program segment that consists of a decision tree.
- These decisions, in various combinations, can lead to actions 1, 2, or 3.
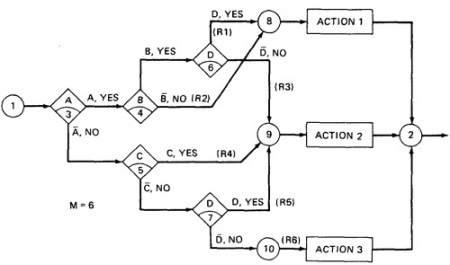
Figure 6.4 : A Sample Program
- If the decision appears on a path, put in a YES or NO as appropriate.
If the decision does not appear on the path, put in an I,
Rule 1 does not contain decision C, therefore its entries are: YES, YES, I, YES.
- The corresponding decision table is shown in Table 6.1
| RULE 1 | RULE 2 | RULE 3 | RULE 4 | RULE 5 | RULE 6 |
|---|
CONDITION A
CONDITION B
CONDITION C
CONDITION D |
YES
YES
I
YES | YES
NO
I
I | YES
YES
I
NO | NO
I
YES
I | NO
I
NO
YES | NO
I
NO
NO |
ACTION 1
ACTION 2
ACTION 3 |
YES
NO
NO | YES
NO
NO | NO
YES
NO | NO
YES
NO | NO
YES
NO | NO
NO
YES |
Table 6.1 : Decision Table corresponding to Figure 6.4
- As an example, expanding the immaterial cases results as below:
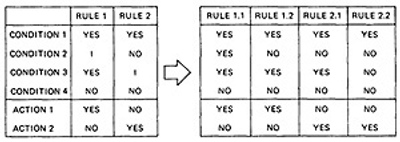
- Similalrly, If we expand the immaterial cases for the above Table 6.1, it results in Table 6.2 as below:
| R 1 | RULE 2 | R 3 | RULE 4 | R 5 | R 6 |
|---|
CONDITION A
CONDITION B
CONDITION C
CONDITION D |
YY
YY
YN
YY | YYYY
NNNN
NNYY
YNNY | YY
YY
YN
NN |
NNNN
YYNN
YYYY
NYYN | NN
NY
NN
YY | NN
YN
NN
NN |
Table 6.2 : Expansion of Table 6.1
- Sixteen cases are represented in Table 6.1, and no case appears twice.
- Consequently, the flowgraph appears to be complete and consistent.
- As a first check, before you look for all sixteen combinations, count the number of Y's and N's in each row. They should be equal. We can find the bug that way.
- ANOTHER EXAMPLE - A TROUBLE SOME PROGRAM:
- Consider the following specification whose putative flowgraph is shown in Figure 6.5:
- If condition A is met, do process A1 no matter what other actions are taken or what other conditions are met.
- If condition B is met, do process A2 no matter what other actions are taken or what other conditions are met.
- If condition C is met, do process A3 no matter what other actions are taken or what other conditions are met.
- If none of the conditions is met, then do processes A1, A2, and A3.
- When more than one process is done, process A1 must be done first, then A2, and then A3. The only permissible cases are: (A1), (A2), (A3), (A1,A3), (A2,A3) and (A1,A2,A3).
- Figure 6.5 shows a sample program with a bug.
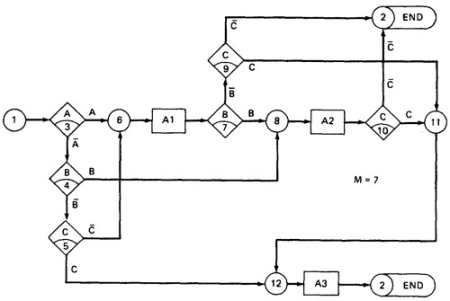
Figure 6.5 : A Troublesome Program
- The programmer tried to force all three processes to be executed for the
 cases but forgot that the B and C predicates would be done again, thereby bypassing processes A2 and A3. cases but forgot that the B and C predicates would be done again, thereby bypassing processes A2 and A3.
- Table 6.3 shows the conversion of this flowgraph into a decision table after expansion.
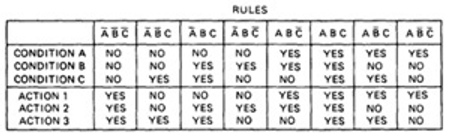
Table 6.3 : Decision Table for Figure 6.5
PATH EXPRESSIONS:
- GENERAL:
- Logic-based testing is structural testing when it's applied to structure (e.g., control flowgraph of an implementation);
it's functional testing when it's applied to a specification.
- In logic-based testing we focus on the truth values of control flow predicates.
- A predicate is implemented as a process whose outcome is a truth-functional value.
- For our purpose, logic-based testing is restricted to binary predicates.
- We start by generating path expressions by path tracing as in Unit V, but this time, our purpose is to convert the path expressions into boolean algebra,
using the predicates' truth values (e.g., A and
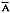 ) as weights. ) as weights.
- BOOLEAN ALGEBRA:
- STEPS:
- Label each decision with an uppercase letter that represents the truth value of the predicate. The YES or TRUE branch is labeled with a letter (say A) and the NO or FALSE branch with the same letter overscored (say
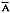 ). ).
- The truth value of a path is the product of the individual labels. Concatenation or products mean "AND". For example, the straight-through path of Figure 6.5, which goes via nodes 3, 6, 7, 8, 10, 11, 12, and 2, has a truth value of ABC.
The path via nodes 3, 6, 7, 9 and 2 has a value of
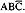 . .
- If two or more paths merge at a node, the fact is expressed by use of a plus sign (+) which means "OR".

Figure 6.5 : A Troublesome Program
- Using this convention, the truth-functional values for several of the nodes can be expressed in terms of segments from previous nodes. Use the node name to identify the point.
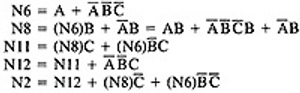
- There are only two numbers in boolean algebra: zero (0) and one (1). One means "always true" and zero means "always false".
- RULES OF BOOLEAN ALGEBRA:
- Boolean algebra has three operators: X (AND), + (OR) and
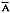 (NOT) (NOT)
- X : meaning AND. Also called multiplication. A statement such as AB (A X B) means "A and B are both true". This symbol is usually left out as in ordinary algebra.
- + : meaning OR. "A + B" means "either A is true or B is true or both".
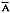 meaning NOT. Also negation or complementation. This is read as either "not A" or "A bar". The entire expression under the bar is negated. meaning NOT. Also negation or complementation. This is read as either "not A" or "A bar". The entire expression under the bar is negated.- The following are the laws of boolean algebra:

- In all of the above, a letter can represent a single sentence or an entire boolean algebra expression.
- Individual letters in a boolean algebra expression are called Literals (e.g. A,B)
- The product of several literals is called a product term (e.g., ABC, DE).
- An arbitrary boolean expression that has been multiplied out so that it consists of the sum of products (e.g., ABC + DEF + GH) is said to be in sum-of-products form.
- The result of simplifications (using the rules above) is again in the sum of product form and each product term in such a simplified version is called a prime implicant.
For example, ABC + AB + DEF reduces by rule 20 to AB + DEF; that is, AB and DEF are prime implicants.
- The path expressions of Figure 6.5 can now be simplified by applying the rules.
- The following are the laws of boolean algebra:

- Similarly,

- The deviation from the specification is now clear. The functions should have been:
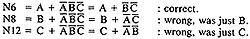
- Loops complicate things because we may have to solve a boolean equation to determine what predicate-value combinations lead to where.
KV CHARTS:
- INTRODUCTION:
- If you had to deal with expressions in four, five, or six variables,
you could get bogged down in the algebra and make as many errors in designing test cases as there are bugs in the routine you're testing.
- Karnaugh-Veitch chart reduces boolean algebraic manipulations to graphical trivia.
- Beyond six variables these diagrams get cumbersome and may not be effective.
- SINGLE VARIABLE:
- Figure 6.6 shows all the boolean functions of a single variable and their equivalent representation as a KV chart.
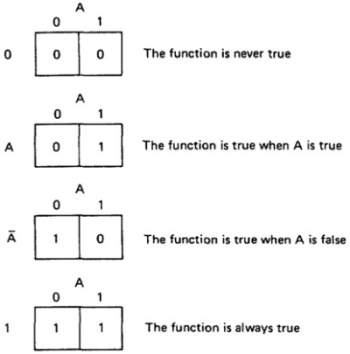
Figure 6.6 : KV Charts for Functions of a Single Variable.
- The charts show all possible truth values that the variable A can have.
- A "1" means the variable’s value is "1" or TRUE. A "0" means that the variable's value is 0 or FALSE.
- The entry in the box (0 or 1) specifies whether the function that the chart represents is true or false for that value of the variable.
- We usually do not explicitly put in 0 entries but specify only the conditions under which the function is true.
- TWO VARIABLES:
- Figure 6.7 shows eight of the sixteen possible functions of two variables.
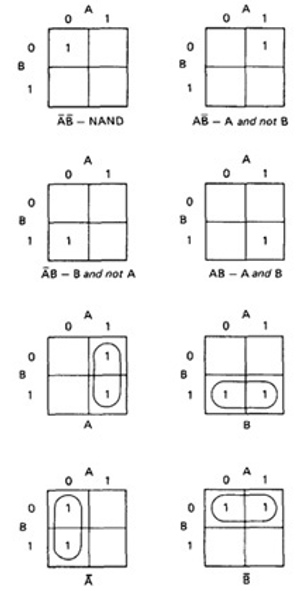
Figure 6.7 : KV Charts for Functions of Two Variables.
- Each box corresponds to the combination of values of the variables for the row and column of that box.
- A pair may be adjacent either horizontally or vertically but not diagonally.
- Any variable that changes in either the horizontal or vertical direction does not appear in the expression.
- In the fifth chart, the B variable changes from 0 to 1 going down the column, and because the A variable's value for the column is 1, the chart is equivalent to a simple A.
- Figure 6.8 shows the remaining eight functions of two variables.
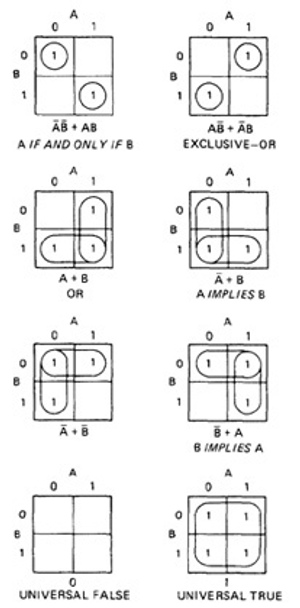
Figure 6.8 : More Functions of Two Variables.
- The first chart has two 1's in it, but because they are not adjacent, each must be taken separately.
- They are written using a plus sign.
- It is clear now why there are sixteen functions of two variables.
- Each box in the KV chart corresponds to a combination of the variables' values.
- That combination might or might not be in the function (i.e., the box corresponding to that combination might have a 1 or 0 entry).
- Since n variables lead to 2n combinations of 0 and 1 for the variables, and each such combination (box) can be filled or not filled, leading to 22n ways of doing this.
- Consequently for one variable there are 221 = 4 functions, 16 functions of 2 variables, 256 functions of 3 variables, 16,384 functions of 4 variables, and so on.
- Given two charts over the same variables, arranged the same way, their product is the term by term product, their sum is the term by term sum, and the negation of a chart is gotten by reversing all the 0 and 1 entries in the chart.
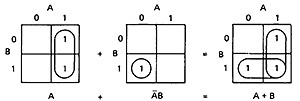
OR
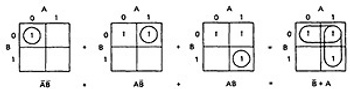
- THREE VARIABLES:
- KV charts for three variables are shown below.
- As before, each box represents an elementary term of three variables with a bar appearing or not appearing according to whether the row-column heading for that box is 0 or 1.
- A three-variable chart can have groupings of 1, 2, 4, and 8 boxes.
- A few examples will illustrate the principles:
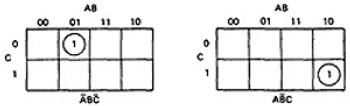
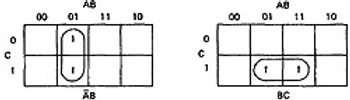
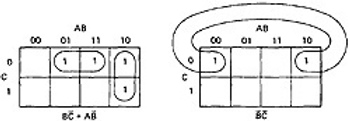
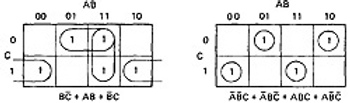
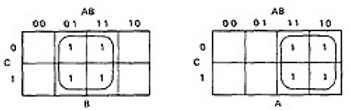
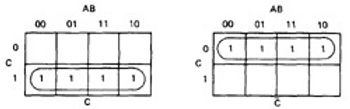
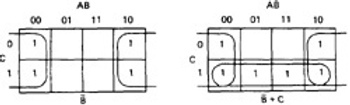
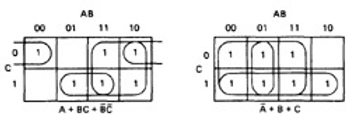
Figure 6.8 : KV Charts for Functions of Three Variables.
- You'll notice that there are several ways to circle the boxes into maximum-sized covering groups.
- FOUR VARIABLES AND MORE:
- The same principles hold for four and more variables.
-
To be added
SPECIFICATIONS:
To be added
SUMMARY:
To be added
|
