QUICK LINKS
BRIEF OVERVIEW
UNIT I
Purpose of Testing
Dichotomies
Model for Testing
Consequences of Bugs
Taxonomy of Bugs
Summary
UNIT II
Basics of Path Testing
Predicates, Path Predicates and Achievable Paths
Path Sensitizing
Path Instrumentation
Application of Path Testing
Summary
UNIT III
Transaction Flows
Transaction Flow Testing Techniques
Implementation
Basics of Data Flow Testing
Strategies in Data Flow Testing
Application of Data Flow Testing
Summary
UNIT IV
Domains and Paths
Nice and Ugly domains
Domain Testing
Domain and Interface Testing
Domains and Testability
Summary
UNIT V
Path products and Path expression
Reduction Procedure
Applications
Regular Expressions and Flow Anomaly Detection
Summary
UNIT VI
Logic Based Testing
Decision Tables
Path Expressions
KV Charts
Specifications
Summary
|
PATHS, PATH PRODUCTS AND REGULAR EXPRESSIONS
This unit gives an indepth overview of Paths of various flow graphs, their interpretations and application.
At the end of this unit, the student will be able to:
- Interpret the control flowgraph and identify the path products, path sums and path expressions.
- Identify how the mathematical laws (distributive, associative, commutative etc) holds for the paths.
- Apply reduction procedure algorithm to a control flowgraph and simplify it into a single path expression.
- Find the all possible paths (Max. Path Count) of a given flow graph.
- Find the minimum paths required to cover a given flow graph.
- Calculate the probability of paths and understand the need for finding the probabilities.
- Differentiate betweeen Structured and Un-structured flowgraphs.
- Calculate the mean processing time of a routine of a given flowgraph.
- Understand how complimentary operations such as PUSH / POP or GET / RETURN are interpreted in a flowgraph.
- Identify the limitations of the above approaches.
- Understand the problems due to flow-anomalies and identify whether anomalies exist in the given path expression.
PATH PRODUCTS AND PATH EXPRESSION:
- MOTIVATION:
- Flow graphs are being an abstract representation of programs.
- Any question about a program can be cast into an equivalent question about an appropriate flowgraph.
- Most software development, testing and debugging tools use flow graphs analysis techniques.
- PATH PRODUCTS:
- Normally flow graphs used to denote only control flow connectivity.
- The simplest weight we can give to a link is a name.
- Using link names as weights, we then convert the graphical flow graph into an equivalent algebraic like expressions
which denotes the set of all possible paths from entry to exit for the flow graph.
- Every link of a graph can be given a name.
- The link name will be denoted by lower case italic letters.
- In tracing a path or path segment through a flow graph, you traverse a succession of link names.
- The name of the path or path segment that corresponds to those links is expressed naturally by concatenating those link names.
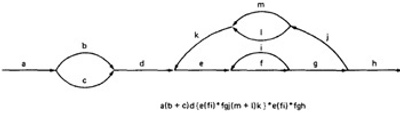
- For example, if you traverse links a,b,c and d along some path, the name for that path segment is abcd. This path name is also called a path product.
Figure 5.1 shows some examples:
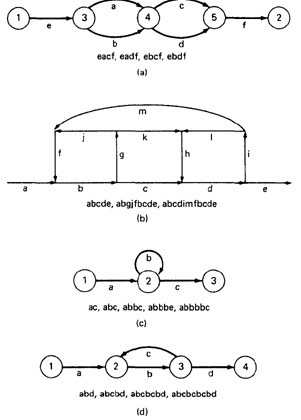
Figure 5.1: Examples of paths.
- PATH EXPRESSION:
- Consider a pair of nodes in a graph and the set of paths between those node.
- Denote that set of paths by Upper case letter such as X,Y. From Figure 5.1c, the members of the path set can be listed as follows:
ac, abc, abbc, abbbc, abbbbc.............
- Alternatively, the same set of paths can be denoted by :
ac+abc+abbc+abbbc+abbbbc+...........
- The + sign is understood to mean "or" between the two nodes of interest, paths ac, or abc, or abbc, and so on can be taken.
- Any expression that consists of path names and "OR"s and which denotes a set of paths between two nodes is called a "Path Expression.".
- PATH PRODUCTS:
- The name of a path that consists of two successive path segments is conveniently expressed by the concatenation or Path Product of the segment names.
- For example, if X and Y are defined as X=abcde,Y=fghij,then the path corresponding to X followed by Y is denoted by
XY=abcdefghij
- Similarly,
YX=fghijabcde
aX=aabcde
Xa=abcdea
XaX=abcdeaabcde
- If X and Y represent sets of paths or path expressions, their product represents the set of paths that can be obtained by following every element of X by any element of Y in all possible ways. For example,
X = abc + def + ghi
Y = uvw + z
Then,
XY = abcuvw + defuvw + ghiuvw + abcz + defz + ghiz
- If a link or segment name is repeated, that fact is denoted by an exponent. The exponent's value denotes the number of repetitions:
a1 = a; a2 = aa; a3 = aaa; an = aaaa . . . n times.
Similarly, if
X = abcde
then
X1 = abcde
X2 = abcdeabcde = (abcde)2
X3 = abcdeabcdeabcde = (abcde)2abcde
= abcde(abcde)2 = (abcde)3
- The path product is not commutative (that is XY!=YX).
- The path product is Associative.
RULE 1: A(BC)=(AB)C=ABC
where A,B,C are path names, set of path names or path expressions.
- The zeroth power of a link name, path product, or path expression is also needed for completeness. It is denoted by the numeral "1" and denotes the "path" whose length is zero
- that is, the path that doesn't have any links.
a0 = 1
X0 = 1
- PATH SUMS:
- DISTRIBUTIVE LAWS:
- ABSORPTION RULE:
- LOOPS:
- Loops can be understood as an infinite set of parallel paths. Say that the loop consists of a single link b. then the set of all paths through that loop point is b0+b1+b2+b3+b4+b5+..............
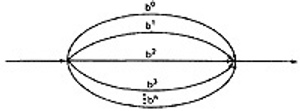
Figure 5.3: Examples of path loops.
- This potentially infinite sum is denoted by b* for an individual link and by X* when X is a path expression.
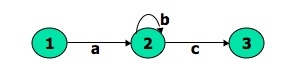
Figure 5.4: Another example of path loops.
- The path expression for the above figure is denoted by the notation:
ab*c=ac+abc+abbc+abbbc+................
- Evidently,
aa*=a*a=a+ and XX*=X*X=X+
- It is more convenient to denote the fact that a loop cannot be taken more than a certain, say n, number of times.
- A bar is used under the exponent to denote the fact as follows:
Xn = X0+X1+X2+X3+X4+X5+..................+Xn
- RULES 6 - 16:
- The following rules can be derived from the previous rules:
RULE 6: Xn + Xm = Xn if n>m
RULE 6: Xn + Xm = Xm if m>n
RULE 7: XnXm = Xn+m
RULE 8: XnX* = X*Xn = X*
RULE 9: XnX+ = X+Xn = X+
RULE 10: X*X+ = X+X* = X+
RULE 11: 1 + 1 = 1
RULE 12: 1X = X1 = X
Following or preceding a set of paths by a path of zero length does not change the set.
RULE 13: 1n = 1n = 1* = 1+ = 1
No matter how often you traverse a path of zero length,It is a path of zero length.
RULE 14: 1++1 = 1*=1
The null set of paths is denoted by the numeral 0. it obeys the following rules:
RULE 15: X+0=0+X=X
RULE 16: 0X=X0=0
If you block the paths of a graph for or aft by a graph that has no paths , there wont be any paths.
REDUCTION PROCEDURE:
- REDUCTION PROCEDURE ALGORITHM:
- This section presents a reduction procedure for converting a flowgraph
whose links are labeled with names into a path expression that denotes the set of all entry/exit paths in that flowgraph.
The procedure is a node-by-node removal algorithm.
- The steps in Reduction Algorithm are as follows:
- Combine all serial links by multiplying their path expressions.
- Combine all parallel links by adding their path expressions.
- Remove all self-loops (from any node to itself) by replacing them with a link of the form X*, where X is the path expression of the link in that loop.
STEPS 4 - 8 ARE IN THE ALGORIHTM'S LOOP:
- Select any node for removal other than the initial or final node. Replace it with a set of equivalent links whose path expressions
correspond to all the ways you can form a product of the set of inlinks with the set of outlinks of that node.
- Combine any remaining serial links by multiplying their path expressions.
- Combine all parallel links by adding their path expressions.
- Remove all self-loops as in step 3.
- Does the graph consist of a single link between the entry node and the exit node?
If yes, then the path expression for that link is a path expression for the original flowgraph; otherwise, return to step 4.
- A flowgraph can have many equivalent path expressions between a given pair of nodes;
that is, there are many different ways to generate the set of all paths between two nodes without affecting the content of that set.
- The appearance of the path expression depends, in general, on the order in which nodes are removed.
- CROSS-TERM STEP (STEP 4):
- LOOP REMOVAL OPERATIONS:
- There are two ways of looking at the loop-removal operation:
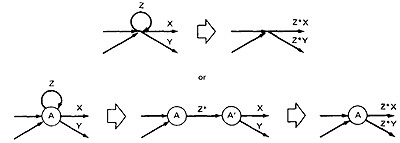
- In the first way, we remove the self-loop and then multiply all outgoing links by Z*.
- In the second way, we split the node into two equivalent nodes, call them A and A' and put in a link between them whose path expression is Z*.
Then we remove node A' using steps 4 and 5 to yield outgoing links whose path expressions are Z*X and Z*Y.
- A REDUCTION PROCEDURE - EXAMPLE:
APPLICATIONS:
- APPLICATIONS:
- The purpose of the node removal algorithm is to present one very generalized concept- the path expression and way of getting it.
- Every application follows this common pattern:
- Convert the program or graph into a path expression.
- Identify a property of interest and derive an appropriate set of "arithmetic" rules that characterizes the property.
- Replace the link names by the link weights for the property of interest. The path expression has now been converted to an expression in
some algebra, such as ordinary algebra, regular expressions, or boolean algebra. This algebraic expression summarizes the property of interest over the set of all paths.
- Simplify or evaluate the resulting "algebraic" expression to answer the question you asked.
- HOW MANY PATHS IN A FLOWGRAPH ?
- The question is not simple. Here are some ways you could ask it:
- What is the maximum number of different paths possible?
- What is the fewest number of paths possible?
- How many different paths are there really?
- What is the average number of paths?
- Determining the actual number of different paths is an inherently difficult problem because there could be unachievable paths resulting from correlated and dependent predicates.
- If we know both of these numbers (maximum and minimum number of possible paths) we have a good idea of how complete our testing is.
- Asking for "the average number of paths" is meaningless.
- MAXIMUM PATH COUNT ARITHMETIC:
- Label each link with a link weight that corresponds to the number of paths that link represents.
- Also mark each loop with the maximum number of times that loop can be taken.
If the answer is infinite, you might as well stop the analysis because it is clear that the maximum number of paths will be infinite.
- There are three cases of interest: parallel links, serial links, and loops.
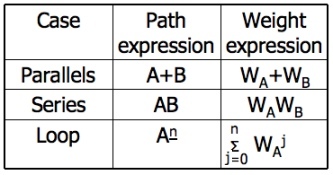
- This arithmetic is an ordinary algebra. The weight is the number of paths in each set.
- EXAMPLE:
- Alternatively, you could have substituted a "1" for each link in the path expression and then simplified, as follows:
a(b+c)d{e(fi)*fgj(m+l)k}*e(fi)*fgh
= 1(1 + 1)1(1(1 x 1)31 x 1 x 1(1 + 1)1)41(1 x 1)31 x 1 x 1
= 2(131 x (2))413
= 2(4 x 2)4 x 4
= 2 x 84 x 4
= 32,768
- This is the same result we got graphically.
- Actually, the outer loop should be taken exactly four times. That doesn't mean it will be taken zero or four times.
Consequently, there is a superfluous "4" on the outlink in the last step. Therefore the maximum number of different paths is 8192 rather than 32,768.
- STRUCTURED FLOWGRAPH:
- Structured code can be defined in several different ways that do not involve ad-hoc rules such as not using GOTOs.
- A structured flowgraph is one that can be reduced to a single link by successive application of the transformations of Figure 5.7.
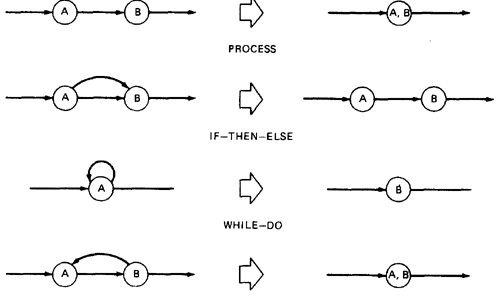
Figure 5.7: Structured Flowgraph Transformations.
- The node-by-node reduction procedure can also be used as a test for structured code.
- Flow graphs that DO NOT contain one or more of the graphs shown below (Figure 5.8) as subgraphs are structured.
- Jumping into loops
- Jumping out of loops
- Branching into decisions
- Branching out of decisions
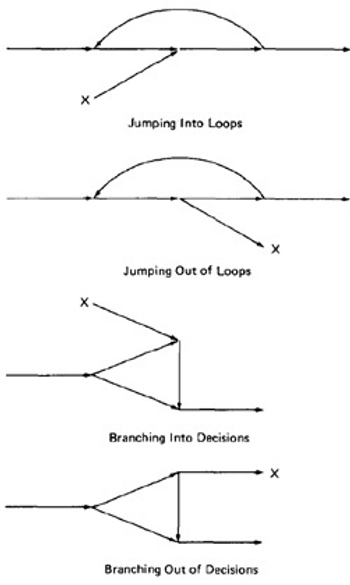
Figure 5.8: Un-structured sub-graphs.
- LOWER PATH COUNT ARITHMETIC:
- A lower bound on the number of paths in a routine can be approximated for structured flow graphs.
- The arithmetic is as follows:
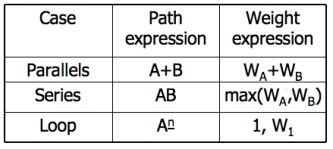
- The values of the weights are the number of members in a set of paths.
- EXAMPLE:
- Applying the arithmetic to the earlier example gives us the identical steps unitl step 3 (C) as below:
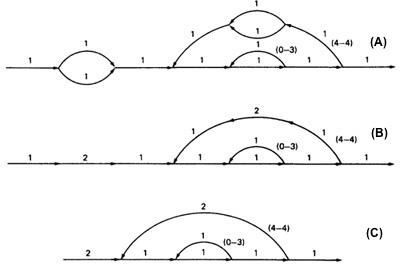
- From Step 4, the it would be different from the previous example:
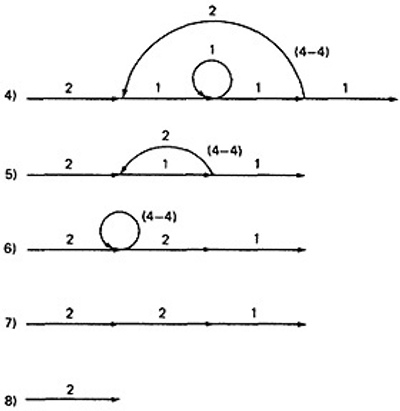
- If you observe the original graph, it takes at least two paths to cover and that it can be done in two paths.
- If you have fewer paths in your test plan than this minimum you probably haven't covered. It's another check.
- CALCULATING THE PROBABILITY:
- Path selection should be biased toward the low - rather than the high-probability paths.
- This raises an interesting question:
What is the probability of being at a certain point in a routine?
This question can be answered under suitable assumptions, primarily that all probabilities involved are independent, which is to say that all decisions are independent and uncorrelated.
- We use the same algorithm as before : node-by-node removal of uninteresting nodes.
- Weights, Notations and Arithmetic:
- Probabilities can come into the act only at decisions (including decisions associated with loops).
- Annotate each outlink with a weight equal to the probability of going in that direction.
- Evidently, the sum of the outlink probabilities must equal 1
- For a simple loop, if the loop will be taken a mean of N times, the looping probability is N/(N + 1) and the probability of not looping is 1/(N + 1).
- A link that is not part of a decision node has a probability of 1.
- The arithmetic rules are those of ordinary arithmetic.
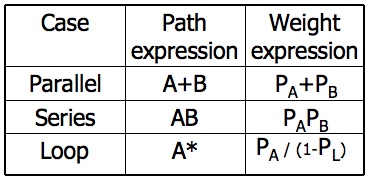
- In this table, in case of a loop, PA is the probability of the link leaving the loop and PL is the probability of looping.
- The rules are those of ordinary probability theory.
- If you can do something either from column A with a probability of PA or from column B with a probability PB, then the probability that you do either is PA + PB.
- For the series case, if you must do both things, and their probabilities are independent (as assumed), then the probability that you do both is the product of their probabilities.
- For example, a loop node has a looping probability of PL and a probability of not looping of PA, which is obviously equal to I - PL.
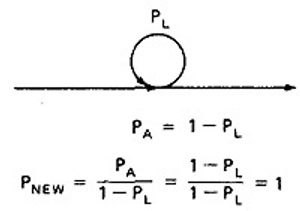
- Following the above rule, all we've done is replace the outgoing probability with 1 - so why the complicated rule? After a few steps in which you've removed nodes,
combined parallel terms, removed loops and the like, you might find something like this:
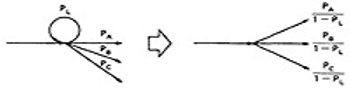
because PL + PA + PB + PC = 1, 1 - PL = PA + PB + PC, and
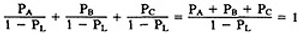
which is what we've postulated for any decision. In other words, division by 1 - PL renormalizes the outlink probabilities so that their sum equals unity after the loop is removed.
- EXAMPLE:
- Here is a complicated bit of logic. We want to know the probability associated with cases A, B, and C.
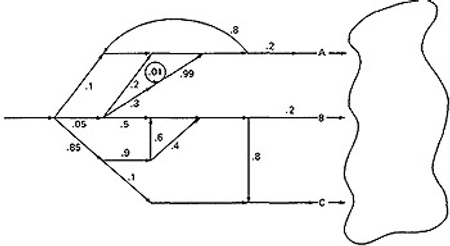
- Let us do this in three parts, starting with case A. Note that the sum of the probabilities at each decision node is equal to 1.
Start by throwing away anything that isn't on the way to case A, and then apply the reduction procedure.
To avoid clutter, we usually leave out probabilities equal to 1.
CASE A:
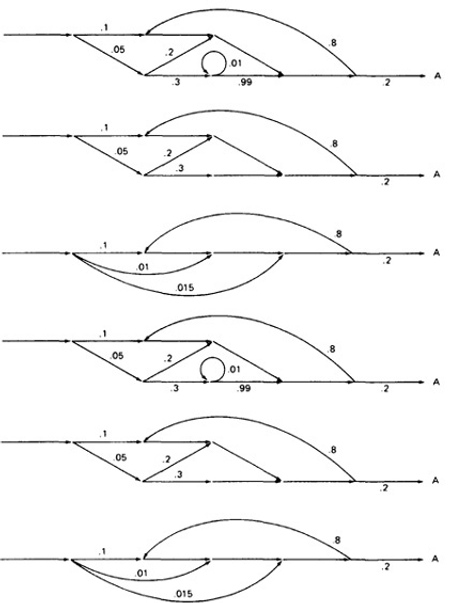
- Case B is simpler:
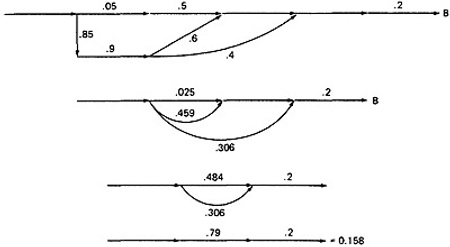
- Case C is similar and should yield a probability of 1 - 0.125 - 0.158 = 0.717:
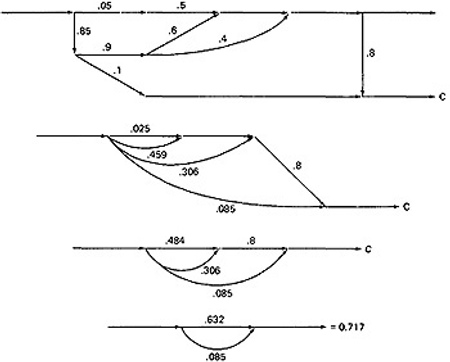
- This checks. It's a good idea when doing this sort of thing to calculate all the probabilities and to verify that the sum of the routine's exit probabilities does equal 1.
- If it doesn't, then you've made calculation error or, more likely, you've left out some branching probability.
- How about path probabilities? That's easy. Just trace the path of interest and multiply the probabilities as you go.
- Alternatively, write down the path name and do the indicated arithmetic operation.
- Say that a path consisted of links a, b, c, d, e, and the associated probabilities were .2, .5, 1., .01, and I respectively. Path abcbcbcdeabddea would have a probability of 5 x 10-10.
- Long paths are usually improbable.
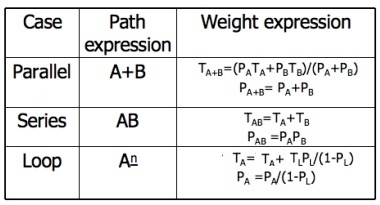
- MEAN PROCESSING TIME OF A ROUTINE:
- Given the execution time of all statements or instructions for every link in a flowgraph and the probability for each direction for all decisions are to find the mean processing time for the routine as a whole.
- The model has two weights associated with every link: the processing time for that link, denoted by T, and the probability of that link P.
- The arithmetic rules for calculating the mean time:
- EXAMPLE:
- Start with the original flow graph annotated with probabilities and processing time.
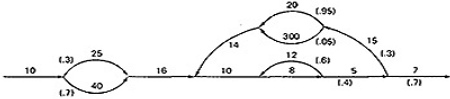
- Combine the parallel links of the outer loop. The result is just the mean of the processing times for the links because there aren't any other links leaving the first node.
Also combine the pair of links at the beginning of the flowgraph..

- Combine as many serial links as you can.
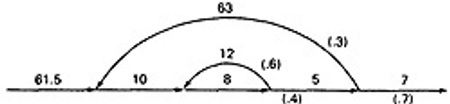
- Use the cross-term step to eliminate a node and to create the inner self - loop.
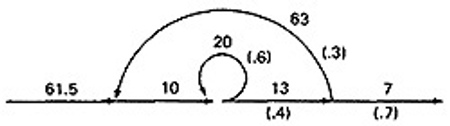
- Finally, you can get the mean processing time, by using the arithmetic rules as follows:
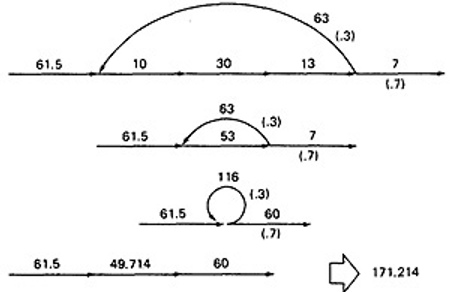
- PUSH/POP, GET/RETURN:
- LIMITATIONS AND SOLUTIONS:
- The main limitation to these applications is the problem of unachievable paths.
- The node-by-node reduction procedure, and most graph-theory-based algorithms work well when all paths are possible,
but may provide misleading results when some paths are unachievable.
- The approach to handling unachievable paths (for any application) is to partition the graph into subgraphs so that all paths in each of the subgraphs are achievable.
- The resulting subgraphs may overlap, because one path may be common to several different subgraphs.
- Each predicate's truth-functional value potentially splits the graph into two subgraphs. For n predicates, there could be as many as 2n subgraphs.
REGULAR EXPRESSIONS AND FLOW ANOMALY DETECTION:
- THE PROBLEM:
- The generic flow-anomaly detection problem (note: not just data-flow anomalies, but any flow anomaly) is that of looking for a specific sequence of options
considering all possible paths through a routine.
- Let the operations be SET and RESET, denoted by s and r respectively, and we want to know if there is a SET followed immediately a SET or
a RESET followed immediately by a RESET (an ss or an rr sequence).
- Some more application examples:
- A file can be opened (o), closed (c), read (r), or written (w). If the file is read or written to after it's been closed, the sequence is nonsensical.
Therefore, cr and cw are anomalous. Similarly, if the file is read before it's been written, just after opening, we may have a bug.
Therefore, or is also anomalous. Furthermore, oo and cc, though not actual bugs, are a waste of time and therefore should also be examined.
- A tape transport can do a rewind (d), fast-forward (f), read (r), write (w), stop (p), and skip (k). There are rules concerning the use of the transport;
for example, you cannot go from rewind to fast-forward without an intervening stop or from rewind or fast-forward to read or write without an intervening stop.
The following sequences are anomalous: df, dr, dw, fd, and fr. Does the flowgraph lead to anomalous sequences on any path?
If so, what sequences and under what circumstances?
- The data-flow anomalies discussed in Unit 4 requires us to detect the dd, dk, kk, and ku sequences. Are there paths with anomalous data flows?
- THE METHOD:
- Annotate each link in the graph with the appropriate operator or the null operator 1.
- Simplify things to the extent possible, using the fact that a + a = a and 12 = 1.
- You now have a regular expression that denotes all the possible sequences of operators in that graph.
You can now examine that regular expression for the sequences of interest.
- EXAMPLE: Let A, B, C, be nonempty sets of character sequences whose smallest string is at least one character long.
Let T be a two-character string of characters. Then if T is a substring of (i.e., if T appears within) ABnC, then T will appear in AB2C. (HUANG's Theorem)
- As an example, let
A = pp
B = srr
C = rp
T = ss
The theorem states that ss will appear in pp(srr)nrp if it appears in pp(srr)2rp.
- However, let
A = p + pp + ps
B = psr + ps(r + ps)
C = rp
T = P4
Is it obvious that there is a p4 sequence in ABnC? The theorem states that we have only to look at
(p + pp + ps)[psr + ps(r + ps)]2rp
Multiplying out the expression and simplifying shows that there is no p4 sequence.
- Incidentally, the above observation is an informal proof of the wisdom of looping twice discussed in Unit 2.
Because data-flow anomalies are represented by two-character sequences, it follows the above theorem that looping twice is what you need to do to find such anomalies.
- LIMITATIONS:
- Huang's theorem can be easily generalized to cover sequences of greater length than two characters.
Beyond three characters, though, things get complex and this method has probably reached its utilitarian limit for manual application.
- There are some nice theorems for finding sequences that occur at the beginnings and ends of strings but no nice algorithms for finding strings buried in an expression.
- Static flow analysis methods can't determine whether a path is or is not achievable. Unless the flow analysis includes symbolic execution or similar techniques, the impact of unachievable paths will not be included in the analysis.
- The flow-anomaly application, for example, doesn't tell us that there will be a flow anomaly - it tells us that if the path is achievable, then there will be a flow anomaly.
Such analytical problems go away, of course, if you take the trouble to design routines for which all paths are achievable.
SUMMARY:
- A flowgraph annotated with link names for every link can be converted into a path expression that represents the set of all paths in that flowgraph. A node-by-node reduction procedure is used.
- By substituting link weights for all links, and using the appropriate arithmetic rules, the path expression is converted into an algebraic expression that can be used to determine the minimum and maximum number of possible paths in a flowgraph, the probability that a given node will be reached, the mean processing time of a routine, and other models.
- With different, suitable arithmetic rules, and by using complementary operators as weights for the links, the path expression can be converted into an expression that denotes, over the set of all possible paths, what the net effect of the routine is.
- With links annotated with the appropriate weights, the path expression is converted into a regular expression that denotes the set of all operator sequences over the set of all paths in a routine. Rules for determining whether a given sequence of operations are possible are given. In other words, we have a generalized flow-anomaly detection method that'll work for data-flow anomalies or any other flow anomaly.
- All flow analysis methods lose accuracy and utility if there are unachievable paths. Expand the accuracy and utility of your analytical tools by designs for which all paths are achievable. Such designs are always possible.
|